初等函数

新东西

新定义

习惯于使用大学数学表示方法表示新定义，可以规范自己的语言

定义域

函数定义：设$D$ 是一个实数集合，对每一个$x\in D$,存在一个对应法则$f$,都能对应唯
一的一个实数 $y$,则这个对应法则$f$称为定义在 $D$ 上的一个函数，记为：$y=f(x)$

有界性

$$\begin{aligned}(1)&\text{有界性:}\quad\forall x\in D\text{,若存在正数}M,\text{ 都有}\mid f(x)\mid\leq M\text{ 成立,则称 }f(x)\text{ 在区间 }D\text{ 上}\\\text{有界。}\end{aligned}$$

反函数（逆映射）

我的通俗理解：
想象我们有一个函数 $f(x)$，它在坐标系中画出了一条曲线。现在，我们要找到这个函数的反函数 $f^{-1}(x)$。

步骤1：坐标系转个90度

首先，想象你把整个坐标系顺时针旋转90度，这样原本的 $x$ 轴就变成了 $y$ 轴，$y$ 轴变成了 $x$ 轴。

步骤2：互换 $x$ 轴和 $y$ 轴

接下来，把 $x$ 轴和 $y$ 轴的名字互换。现在，原本的 $x$ 轴上写的是 $y$ ，$y$ 轴上写的是 $x$。

步骤3：画出反函数

现在，观察原函数 $f(x)$ 的图像。对于图像上的任意一点 $(x, f(x))$，想象有一个点 $(f(x), x)$ 正好在它关于直线 $y = x$ 的对称位置。把所有这样的点连起来，就形成了反函数 $f^{-1}(x)$ 的图像。

总结

简单来说，反函数就像是原函数的图像在直线 $y = x$ 上的镜像。如果原函数的图像是一条曲线，那么反函数的图像就是这条曲线关于 $y = x$ 对称的另一条曲线。

复合函数（复合映射）

其实就是高中的复合函数

反函数，复合函数的标准定义

新函数

三角函数：csc、sec、cot

1. 余割 (Cosecant, csc)

• 名称：余割
• 符号：$\csc$
• 计算方法：在直角三角形中，余割是斜边与邻边的比值，即 $\csc(\theta) = \frac{1}{\sin(\theta)}$。
• 与正弦的关系：$\csc(\theta) = \frac{1}{\sin(\theta)}$

2. 正割 (Secant, sec)

• 名称：正割
• 符号：$\sec$
• 计算方法：在直角三角形中，正割是斜边与对边的比值，即 $\sec(\theta) = \frac{1}{\cos(\theta)}$。
• 与余弦的关系：$\sec(\theta) = \frac{1}{\cos(\theta)}$

3. 余切 (Cotangent, cot)

• 名称：余切
• 符号：$\cot$
• 计算方法：在直角三角形中，余切是对边与邻边的比值，即 $\cot(\theta) = \frac{1}{\tan(\theta)}$。
• 与正切的关系：$\cot(\theta) = \frac{1}{\tan(\theta)}$

图像

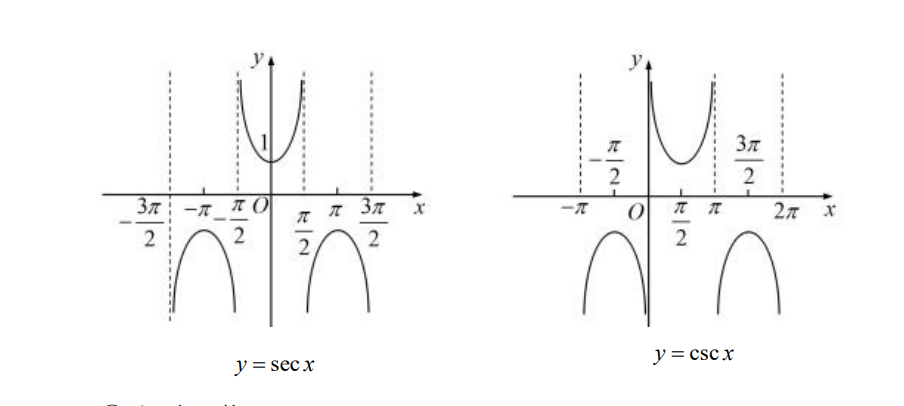
总结

• 这些三角函数都是基本三角函数的倒数：
  • $\csc$ 是 $\sin$ 的倒数
  • $\sec$ 是 $\cos$ 的倒数
  • $\cot$ 是 $\tan$ 的倒数
• 它们在直角三角形中的定义基于斜边与另外两边的比值。
• 它们与正弦、余弦、正切函数的关系是倒数关系

反三角函数（arc什么什么的）

1. 反正弦函数 (Arcsine, $\arcsin$ )

• 名称：反正弦函数
• 符号：$\arcsin(x)$
• 定义域：$x$ 属于 $[-1, 1]$
• 值域：$\arcsin(x)$ 属于 $[- \frac{\pi}{2}, \frac{\pi}{2}]$

2. 反余弦函数 (Arccosine, $\arccos$ )

• 名称：反余弦函数
• 符号：$\arccos(x)$
• 定义域：$x$ 属于 $[-1, 1]$
• 值域：$\arccos(x)$ 属于 $[0, \pi]$

3. 反正切函数 (Arctangent, $\arctan$ )

• 名称：反正切函数
• 符号：$\arctan(x)$
• 定义域：$x$ 属于 $(-\infty, \infty)$（所有实数）
• 值域：$\arctan(x)$ 属于 $(- \frac{\pi}{2}, \frac{\pi}{2})$

图像

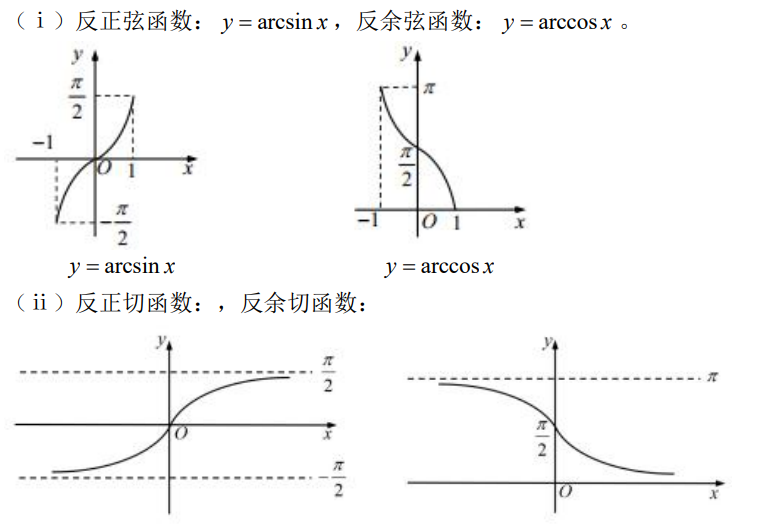
总结

反三角函数是三角函数的逆运算，它们的通用计算方法如下：

• 反三角函数的值通常通过求解基本三角函数的方程来确定。
• 例如，要找到 $\arcsin(x)$，你需要求解 $y$ 使得 $\sin(y) = x$。
• 反三角函数的值通常依赖于自变量的范围，这决定了它们在哪个象限内。
• 反三角函数通常用于求解直角三角形的问题，其中已知一个非直角边和一个角，需要求另一个角。
• 由于反三角函数可能有多值解，实际应用中需要根据特定条件来确定正确的解。

复合函数定义域的注意事项

当求解复合函数的定义域时，需要考虑以下几个关键点：

1. 分母不等于零：

   • 确保函数表达式中的分母没有为零的情况，即 $\frac{1}{x} \neq 0$。

2. 开偶次方的被开方数大于等于零：

   • 对于偶次方根，其被开方数 $a$ 必须满足 $a \geq 0$，即 $\sqrt{x}$ 中的 $x \geq 0$。

3. 对数的真数大于等于零：

   • 对数函数的真数 $b$ 必须满足 $b > 0$，即 $\log_b(x)$ 中的 $x > 0$。

4. 零次方的底数不等于零：

   • 任何非零数的零次方是1，但0的零次方没有定义，因此 $x \neq 0$，即 $x^0$ 中的 $x \neq 0$。

5. 六种基本三角函数的取值范围：

   • 正弦函数 $\sin(x)$ 和余弦函数 $\cos(x)$ 的取值范围是 $[-1, 1]$。
   • 正切函数 $\tan(x)$、余切函数 $\cot(x)$、正割函数 $\sec(x)$ 和余割函数 $\csc(x)$ 没有限制取值范围，但它们在某些特定值处是未定义的。

6. 三种反三角函数的自变量和变量取值范围：

   • 反正弦函数 $\arcsin(x)$ 的自变量 $x$ 取值范围是 $[-1, 1]$，其值域是 $[- \frac{\pi}{2}, \frac{\pi}{2}]$。
   • 反余弦函数 $\arccos(x)$ 的自变量 $x$ 取值范围是 $[-1, 1]$，其值域是 $[0, \pi]$。
   • 反正切函数 $\arctan(x)$ 的自变量 $x$ 可以是所有实数，其值域是 $(- \frac{\pi}{2}, \frac{\pi}{2})$。

在求解复合函数的定义域时，需要综合考虑上述所有条件，以确定函数在整个定义域内都有意义。