极限

感受极限

对于$\text{y=x}$，随着$\text{X}$的无限增大，$\text{y}$的值也会无穷增大
对于$y=x^{2}$，随着$\text{X}$的无限增大，$\text{y}$的值也会无穷增大
对于$\mathbf{y}=\frac1x$，随着$\text{X}$的无限增大，$\text{y}$的值无限接近于0
对于$\mathbf{y}={\frac{\mathbf{x}}{\mathbf{x}+1}}$，随着$\text{X}$的无限增大，$\text{y}$的值无限接近于1

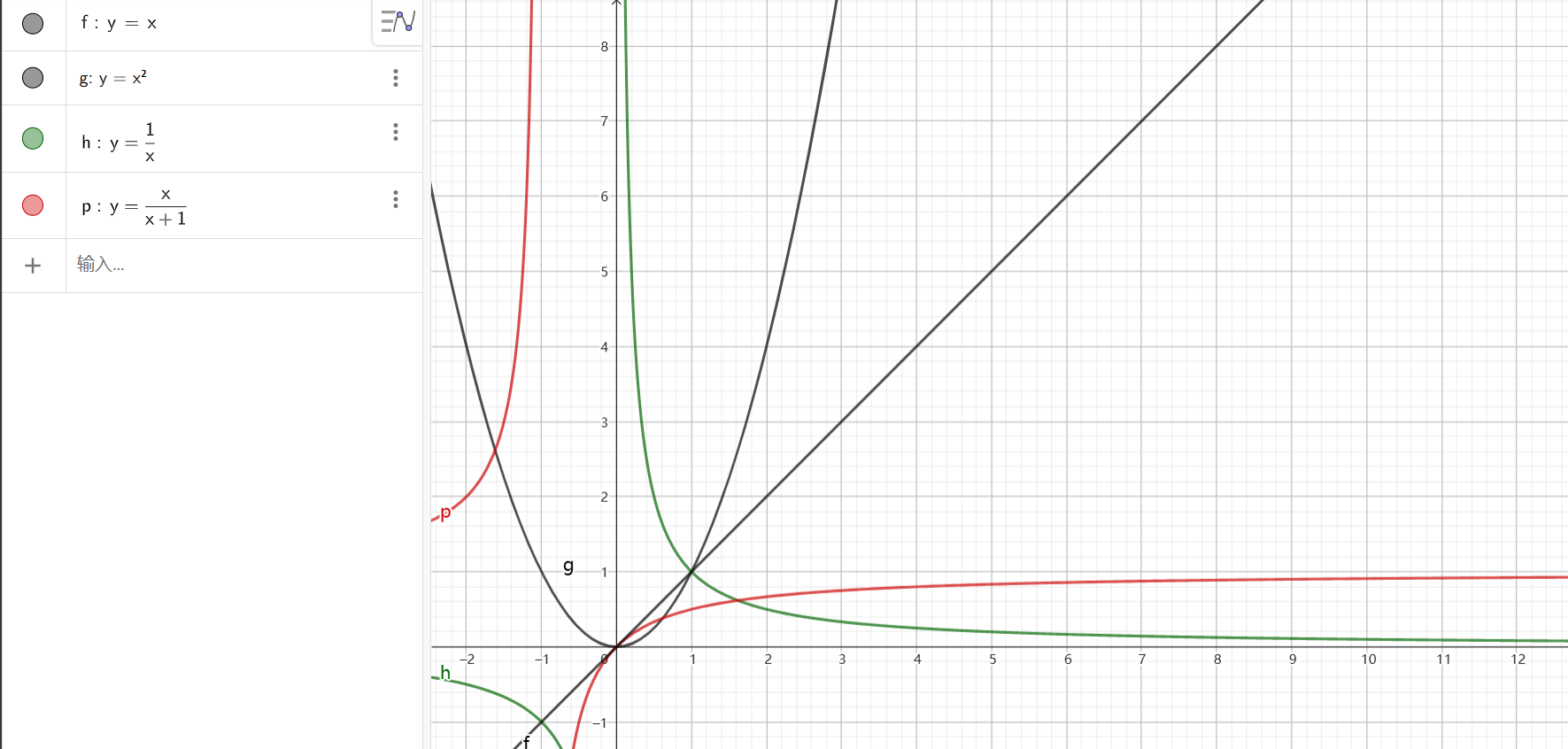
对于$\text{y=x}$，$y=x^{2}$和$\mathbf{y}=\frac1x$的极限结果，都比较好理解
我们来看$\mathbf{y}={\frac{\mathbf{x}}{\mathbf{x}+1}}$是如何计算的
首先在$\text{X}$无限大时$\text{x+1}$也是无限大的，两者都是$+\infty $，
因此在$\text{X}$无限大时，$\text{x=x+1}$是成立的，分子分母相同，求出来就是1（其实这么做不是正确的，因为你不可能写一大段文字描述而且写文字描述也很不数学）

展开看标准计算过程

$$\because\frac{x}{x+1}=\frac{x+1-1}{x+1}=1-\frac{1}{x+1}$$

$\therefore x\rightarrow+\infty $时，

$$\frac{1}{x+1}\rightarrow0\\\therefore\frac{x}{x+1}\rightarrow1$$

标准表示为：$\operatorname*{lim}_{x\rightarrow+\infty}\frac{x}{x+1}=1$

好了，简单求极限就完成了

系统研究极限

考点	重要程度	占分	题型
极限	必考	3~6	选择、填空
极限的性质	★★	0~3	选择、填空
极限的运算法则	必考	基础运算	选择、填空、大题

同济课本

关于教材内容的一个提醒：$1 ,-1 ,1 ,\cdots,( -1 )^{ n+1} ,\cdots ;$这个数列在1和-1之间跳动，没有极限，但是有界

证明极限

方法：

$\forall\varepsilon>0\text{,存在正整数}N\text{,当}n>N\text{时,就有}\left|x_n-A\right|<\varepsilon\text{。}$
简单来说，你先估计一下他的极限（也有可能题目已经给你，要你证明）记作A
然后用通项减去这个A，绝对值要在你给定的这个$\varepsilon $范围内
然后证明反表示的式子是确定的实数
即可

例如
证明数列 $2,\frac12,\frac43,\frac34,\cdots,\frac{n+(-1)^{n-1}}n,\cdots$的极限是1.
证明：

$$|X_{n}-a|=|\frac{n+(-1)^{n-1}-n}{n}|=|\frac{(-1)^{n-1}}{n}|$$ 【先套公式，然后化简】 $$\forall\varepsilon>0,\text{为了使}|x_n-a|<\varepsilon,\text{只要}\frac1n<\varepsilon $$即可 即$$n>\frac{1}{\varepsilon}.$$ 【解出n，反表示法】 这个$\frac{1}{\varepsilon}$是一个确定的实数,而对于任何一个实数都有无穷多个大于它的正整数存在,所以,任取一个大于$\frac{1}{\varepsilon}$的正整数作为N,则当n>N时,就有$\left|\frac{n+(-1)^{n-1}}{n}-1 \right|<\varepsilon $成立【这句话是说$\frac{1}{\varepsilon}$是确定的实数，所以我假设的极限a=1是对的】 即$$\lim_{n\to\infty}\frac{n+( -1 )^{n-1}}{n}=1 .$$

函数极限

上面求的是数列的极限，现在我们要求函数的极限

同济课本

第三方总结

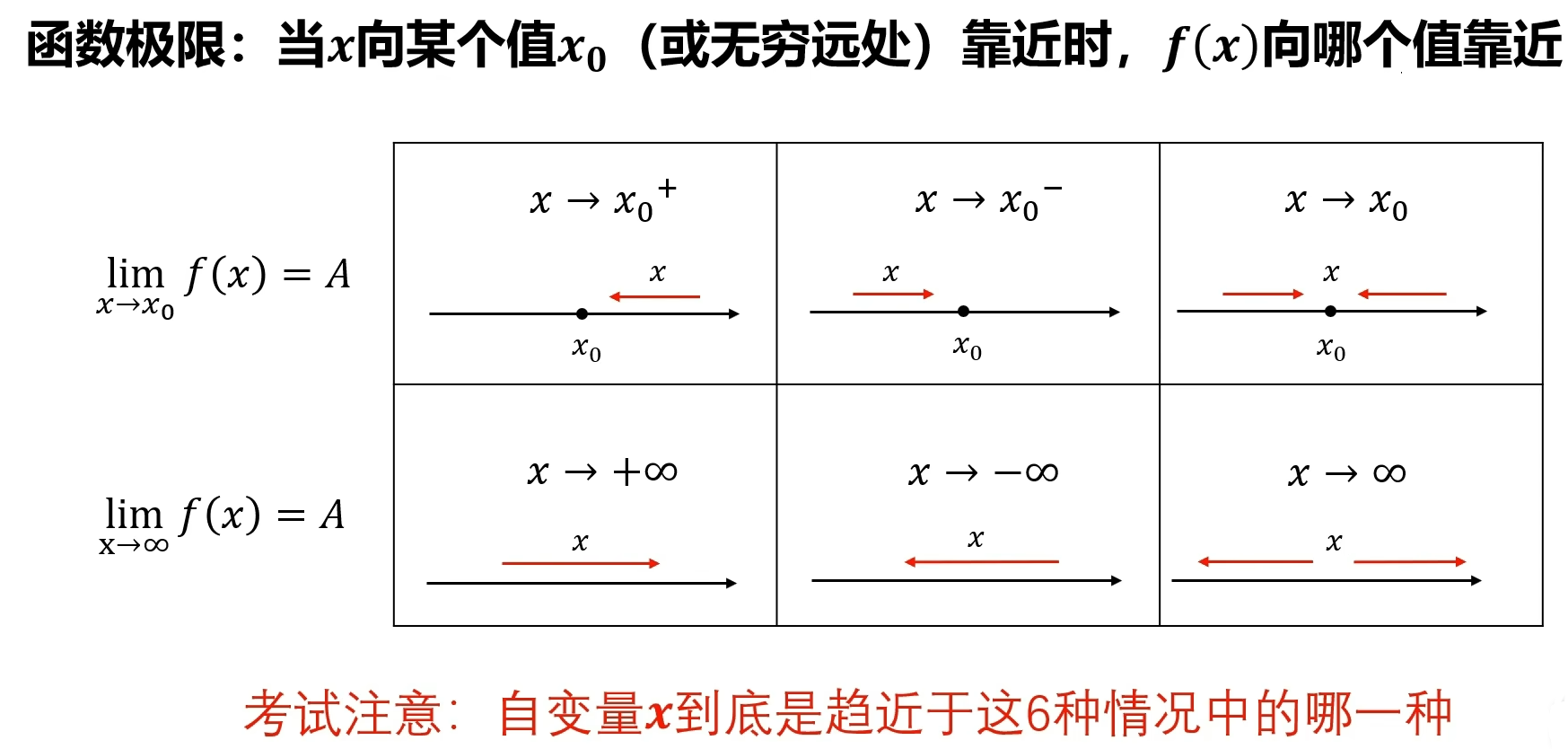
自变量$x$趋于有限值$x_0$时的函数极限

$$\forall\varepsilon>0\text{,存在正数}\delta\text{,当}0<\left|x-x_0\right|<\delta\text{时,就有}\mid f(x)-A\mid<\varepsilon\text{。}$$

看起来又很莫名其妙了
就是要求这个$\lim_{x\to x_0}f(x)=A$
$\lim_{x\to x_0}f(x):x$向某个值靠近时，$f(x)$向哪个值靠近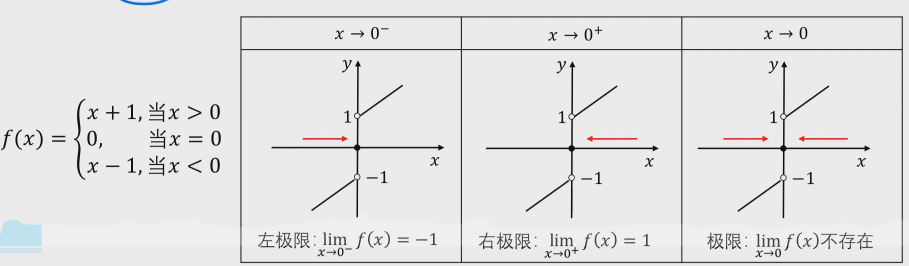

$x\to0^{-}$就是x从左侧靠近0（左极限），$x\to0^{+}$就是x从右侧靠近0（右极限），$x\to0^{}$就是左极限和右极限都求一遍，相等就有不相等就没有

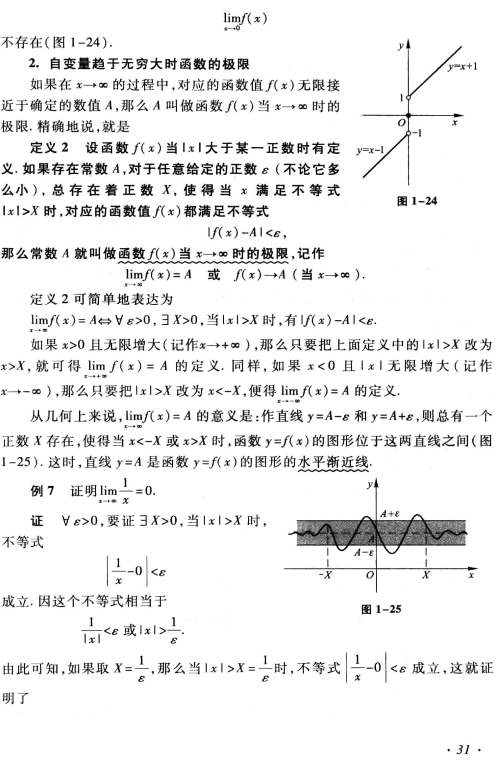
自变量$x$趋于无穷大时的函数极限

定义：如果当$x\to\infty$时，函数$f(x)$无限趋近于某个确定的常数$A$,则称$A$为函数$f(x)$
在$x\to\infty$时的极限，记为$\lim_\mathbf{x}\to\infty f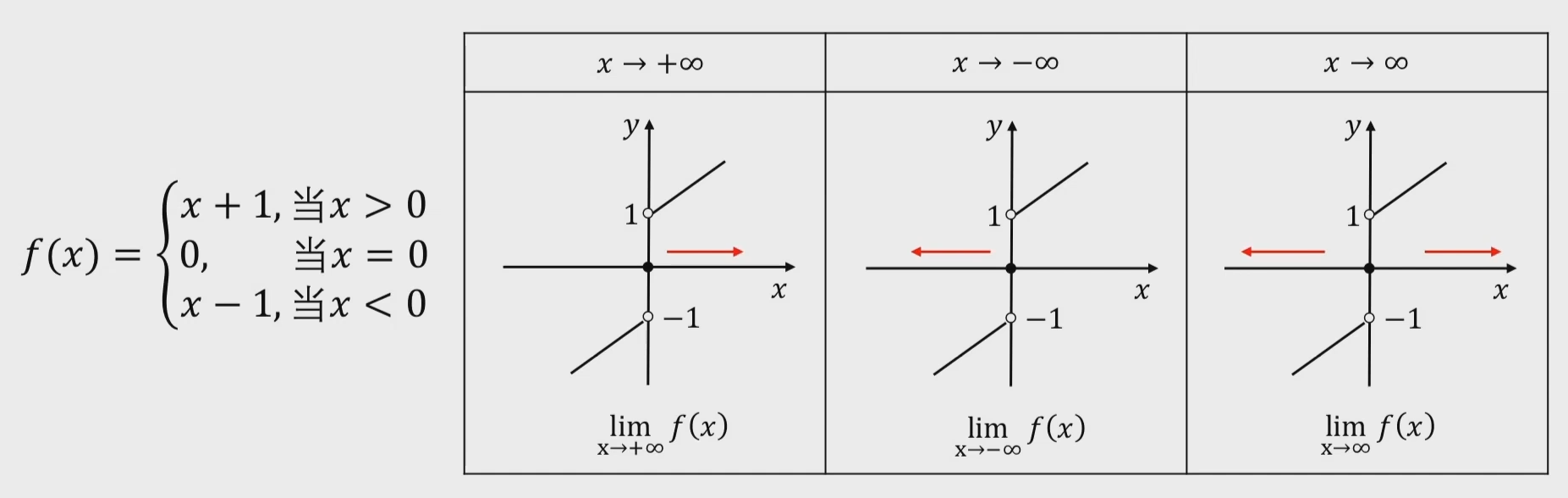(x)=A$ 或$f(x)\to A(x\to\infty)$ 简而言之：$\lim_\mathrm{x\to\infty}f(x):x$向无穷大靠近时，$f(x)$向哪个值靠近

求函数极限

代入法

直接将x的趋近代入式子，然后计算

注意事项

对于代入无法算（0：0）这种应当考虑化简（分母有理化）再求极限

要化简的例子

计算$\lim _x\to 1\frac {x- 1}{\sqrt {x+ 3}- 2}$

解：原式$=\lim_x\to1\frac{(x-1)(\sqrt{x+3}+2)}{(\sqrt{x+3}-2)(\sqrt{x+3}+2)}$

$=\lim_{x\to1}\frac{(x-1)(\sqrt{x+3}+2)}{x-1}$

$=\operatorname*{lim}(\sqrt{x+3}+2)=4$

刷题

$$\lim_{x\to0^-}\frac{e^{\frac1x}+1}{e^{\frac1x}-1}$$ $$x\rightarrow0^{-},\frac{1}{x}\rightarrow-\infty,e^{\frac{1}{x}}\rightarrow0\\\therefore\frac{0+1}{0-1}=\frac{1}{-1}=-1\\即\lim_{x\to0^{-}}\frac{e^{\frac{1}{x}}+1}{e^{\frac{1}{x}}-1}=-1$$

找主干

比如$\lim_{\mathrm{x}\to\infty}\frac{5x^3+3x^2+x}{6x^3+4x^2-x}$
上下极限都是无穷，就要找主要矛盾了
在正无穷和负无穷$x^{3}$对于式子的影响比$x^{2}$和$x$大多了
因此$3x^2+x$和$4x^{2}-x$直接不看
也就是把$x^{3}$给提出来，就像这样

$$\lim_{x\to\infty}\frac{5x^3+3x^2+x}{6x^3+4x^2-x}\\=\lim_{x\to\infty}\frac{x^3(5+\frac2x+\frac1{x^2})}{x^3(6+\frac4x-\frac1{x^2})}$$

所以答案是$\frac56$

一个问题：如果改为趋近于0呢？

答案

那就是$\lim_{x\to0}\frac{x(5x^{2}+3x+1)}{x(6x^{2}+4x-1)}$
这个时候$x$对于式子的影响比$x^{2}$和$x^{3}$大多了，所以提$x$

总结

先找影响最大的项，然后极限就是这两项的比值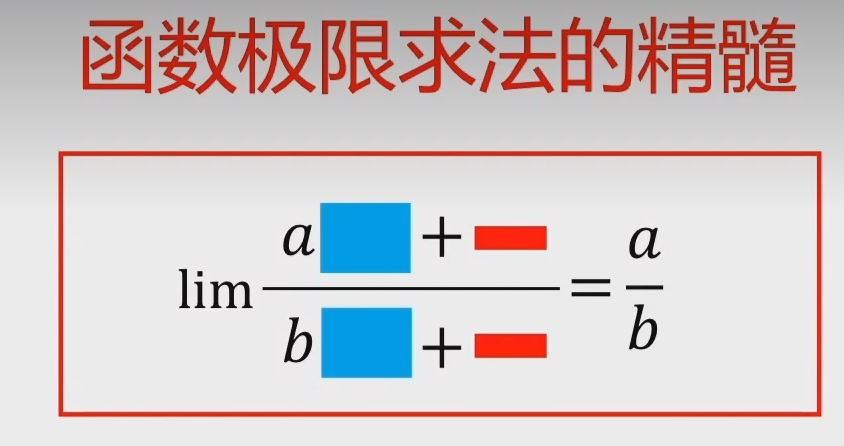

这个是趋近于无穷和具体值都通用的

刷题

刷题